Hello Anyone know of a C Geometry math library?
I need some functions like find Radius and Circle Center from two points on the circumference etc.
Many thanks IMK
Is it even possible to find the radius and centre of a circle given just 2 points on the circumference ?
You need 3.
Hence my question
It took me 5 seconds to find this:
There are many, but I suspect this is an X-Y problem. Assuming the platform is Uno, the answer is "probably not". I mean there is CGAL, I think you will struggle to move that to an Uno. Also I haven't checked, but it may not even have the particular functions you want.
Probably most math libraries assume at least float.
Of course, you would not need a library for that, it's a simple function to implement directly.
You would probably spend more time searching for a library and trying to make it fit than writing the functions you need.
There are an infinite number of circles passing by two points
Problem is some say can do some say can not do.
Hence I look for math library, then i can extract the functions i need.
Bit like the old C Cookbook that had many useful functions but doesn't cover geometry.
Platform is STM32H5 so have loads of space and speed. ![]()
Don’t believe those who say there is only one…
Even if you have two distinct points and the radius there are two circles in 2D space (and an infinite number in 3D space)
If you have three points in 2D and they are non-collinear, there is exactly one circle that can pass through them, but if the points are collinear, no circle can pass through all three points. (In 3D the points would need to be coplanar and non colinear)
Pretty sure there is none that can do, I very much doubt there is a library with new maths no one else has discovered.. Do you have any links?
For only two points, the solution is a line, which needs further data to identify a point.
Yes, "of a circle" but not per se an unique one.
In fact you can choose "a circle" from an infinity sized set of circles.
If you have two points, you can define only one unique circle.
That is the one that has a minimal radius (circumference or area).
It implies the two points are opposite of each other.
The diameter is the distance between the points.
Three points only define a circle if and only if they are not on a straight line.
If you have two points and a radius you can find two circles.
If you have two points and the circumference you can find two circles.
If you have two points and the area you can find two circles.
If you have two points and know they are X degrees apart from the center, will give you two circles.
If you have two points and the distance between the points has a known ratio to the radius, you can find two.
Two points create an arc (chord). Drop a perpendicular to first arc (chord) on the circle. Bisect both perpendiculars (arcs, chords). Intersection is (0, 0).
may be a drawing will be better than a long explanation
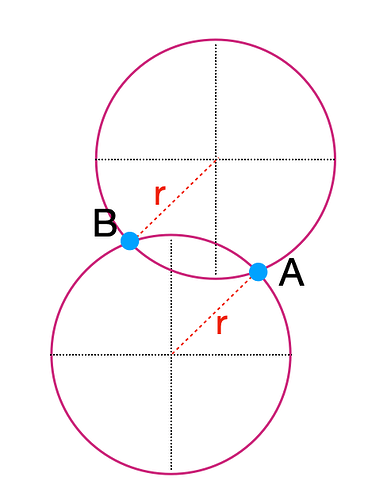
Two points and a radius ➜ 2 circles
Two points, no radius ➜ infinite number of circles
The centers of all these circles lie on a straight line, which is called the perpendicular bisector of the line segment connecting the two points ➜ This happens because for any circle passing through the two points, its center must be equidistant from both points. The only locations that satisfy this condition form a line that is perpendicular to the line connecting the two points and bisects it at its midpoint.
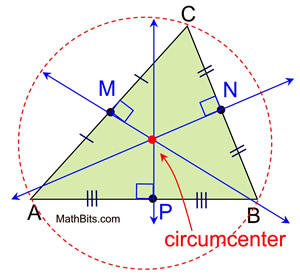
When you have three non-collinear points in 2D, there is exactly one circle that passes through all three points , it's called the circumcircle, and its center is called the circumcenter ➜ the circumcenter is the point where the perpendicular bisectors of the sides of the triangle formed by the three points intersect. The radius of the circumcircle is the distance from the circumcenter to any of the three points.
(this one I got tired and did not draw - comes from here)
From the Trump school of math lol
According to a better math brain than mine:
You can determine a unique steering arc from:
- Robot position
(x₁, y₁) - Target position
(x₂, y₂) - Initial heading (robot's facing direction)
That heading acts like a tangent constraint on the arc. It's what gives us the third input needed to compute a unique circle — specifically, the circle that goes through (x₁, y₁) and (x₂, y₂) with the correct tangent at the start.
I'm going for walk in woods and soak in tube to think about this ![]()
The only perpendiculars that you have are the two that bisect the line joining the two points on the circumference.
The centre of the circle is somewhere on one of those two perpendiculars. Which one do you choose and how do you know where the centre of a particular circle is, bearing in mind that you don't know the radius of the circle ?
Is the discovery of more data not allowed in this? If that third point is not allowed, then i would bisect the initial chord, drop a perpendicular at the bisect point, then make an arbitrary second chord and do the same.
As I said before, 2 points creates a solution that is a line. With the additional tangent, calculate the perpendicular to the tangent, and the line and perpendicular intersect at the center.
There are some edge cases to deal with.
Of course, it is trivial if you already have the circle!