How to smoothen an array of values based on 2 waypoints?

[laptophead]

My math is weak, hope to get some help from someone .

I am building a robot and I am looking for smooth motion.
I developed an micro steps generating function based on:
Encoder reading- the origin of motion,
First Waypoint to go (degrees)
Microsteps to the first Waypoint - int
Second Waypoint
Microsteps to the Second waypoint.

I am getting a good micro steps but the motion is rude and jerky because is linear.
All smoothing libraries are referring to an analog input so I can't feed my micro steps array...

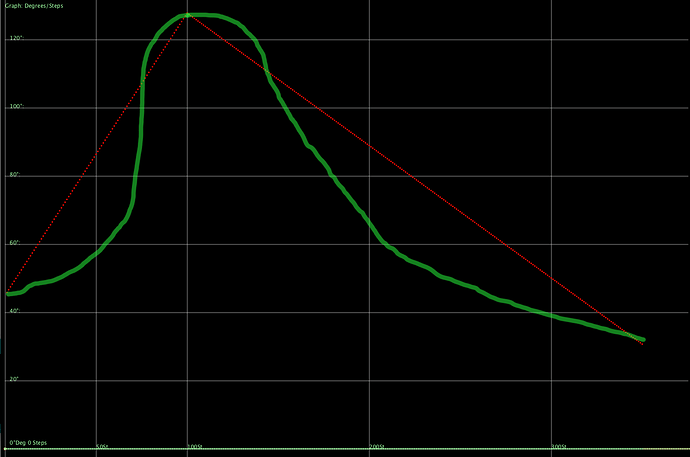
See attached pic, the red is the micro steps generated, the green would be the motion I would like, (Drawn by hand)
Thanks a lot, I know this is not easy....

int Inc;
float EncoderRead = 45;
float GoTo_Gauss [20] [1001];  // motor no, steps no
int Calc_Once = 0;


void setup() {
   Serial.begin(921600); //115200);
    Serial5.begin(115200);


}

void loop() {
  while   (Serial.available () > 0 ) // receiving stuff from keyboard - Serial monitor
  {
    unsigned long SerStamp = millis();
    Serial.println (SerStamp);
    String Kbd_Str = Serial.readStringUntil('\n');
    char FirstKbd = Kbd_Str.charAt(0);


    if (FirstKbd == 'd')
    {
      Linear_Calc_2_W_Pnt (100,  127.76, 250,  30.699, 13 );
    }
  }

}

void Linear_Calc_2_W_Pnt (int MS0,  float Tar0, int MS1,  float Tar1, int motor_id ) // No of steps, Encoder Position, target, motor id

{ //Serial.print (millis());
  Inc = MS0 + MS1;
  float Enc = EncoderRead;

  float Adj_Tar = Tar0 - Enc; //Distance from current postion to the first target
  //Serial.println (Adj_Tar);
  float  I_0 = Adj_Tar / MS0; // this is the increment of each step first segme
  float  I_1 = (Tar0 - Tar1) / MS1; // this is the increment of each step secont segment
  for (int i = 1; i <= Inc; ++i) {

    if (i <= MS0)
    {
      GoTo_Gauss[motor_id][i] = (I_0 * i) + Enc;
    }

    else if (i > MS0)
    { 
      GoTo_Gauss[motor_id][i] = Tar0 - (I_1 * (i - MS0)) ;
    }
    //Serial.println (GoTo_Gauss[motor_id][i], 4);
    Serial5.printf ( "P%.3f  %d  \n",  GoTo_Gauss[motor_id][i] , i);  // array goes to Processing for plotting
    Serial.printf ( "P%.3f  %d  \n",  GoTo_Gauss[motor_id][i] , i);
  }
}

I am running this on a teensy 4.1

[wildbill]

What's the criteria for the smoothing?

[anon57585045]

"Dollars to donuts", I bet this request is for an accel/decel curve. A sin² function would be great for that... but the code is too opaque to speak to.

[J-M-L]

you know three sets of points (x,y) being on the curve (where you are plus your two way points) then If you take a second degree equation (quadratic equation) like this
y = ax² + bx + c
Then you can (generally) find a,b and c. It’s a simple 3 equations / 3 unknown thingy and you’ll find documentation on the solution all over the web.

Then once you have the coefficients it’s just a matter of changing x in small steps (sort the X increasingly or decreasingly) and calculate the associated y and move there. The smaller the deltaX the smoother the interpolation

[laptophead]

void Linear_Calc_2_W_Pnt (int MS0,  float Tar0, int MS1,  float Tar1, int motor_id ) // No of steps, Encoder Position, target, motor id

{ //Serial.print (millis());
  Inc = MS0 + MS1;
  float Enc = EncoderRead;

  float Adj_Tar = Tar0 - Enc; //Distance from current postion to the first target
  //Serial.println (Adj_Tar);
  float exp_coeff_0 = 2.3 / MS0;
  float exp_coeff_1 = 2.3 / MS1;
  Serial.print ("exp_coeff_1= ");
  Serial.println (exp_coeff_1,6);
  float  I_0 = Adj_Tar / MS0; // this is the increment of each step first segme
  float  I_1 = (Tar0 - Tar1) / MS1; // this is the increment of each step secont segment
  for (int i = 1; i <= Inc; ++i) {

    if (i <= MS0)
    {//void GaussCalc (MS0,  float Tar, int motor_id )
      //GoTo_Gauss[motor_id][i] = (I_0 * i) + Enc;
          float x = exp_coeff_0 * i;
            Serial.println (x);
    GoTo_Gauss[motor_id][i] = (Adj_Tar  * (1 - exp(-1 * x * x))) + Enc;
    
    }

    else if (i > MS0)
    {       float x = exp_coeff_1 * (i-MS0);
            Serial.println (x);
    GoTo_Gauss[motor_id][i] = GoTo_Gauss[motor_id][MS0] - ((Tar0 - Tar1)  * (1 - exp(-1 * x * x)));  // ((Tar0 - Tar1)  * (1 - exp(-1 * x * x))) +Tar1 ;
      Serial.printf ( "R%.4f  %d  \n", ((1 - (exp(-1 * x * x)))) , i-MS0);  
      
      //GoTo_Gauss[motor_id][i] = Tar0 - (I_1 * (i - MS0)) ;
    }
    //Serial.println (GoTo_Gauss[motor_id][i], 4);
    Serial5.printf ( "P%.3f  %d  \n",  GoTo_Gauss[motor_id][i] , i);  // array goes to Processing for plotting
    //Serial.printf ( "P%.3f  %d  \n",  GoTo_Gauss[motor_id][i] , i);
  }
}

I think I figured it, looks nice
Thanks JML , Did you mean this also?

[J-M-L]

Using a matrix package can make those things “simple” - there are some for arduino

the idea is that if you have to solve A.X = B then you have X = A^-1.B and this works with Matrix representation of your system if you read about linear algebra.

So if you have a package able to inverse a matrix, then this is pretty easy.

To apply this to your case

you have 3 points A, B and C in 2D space and you look for a b and c such as your three points are on the curve defined by the equation

y = a.x[sup]2[/sup] + b.x + c

Here is an example using BasicLinearAlgebra.h

#include <BasicLinearAlgebra.h> // https://github.com/tomstewart89/BasicLinearAlgebra
using namespace BLA;

struct t_2DPoint {
  float x;
  float y;
};

const t_2DPoint pointA = {3, 12};
const t_2DPoint pointB = {5, 30};
const t_2DPoint pointC = {14, 12};

// looking for a b and c in  y = ax2 + bx + c
// for the quadratic curve going through points A B and C
// system of 3 equations
// 9a + 3b + c = 12
// 25a + 5b + c = 30
// 196a + 14b + c = 12

//      a
// X =  b
//      c
// M . X = R
// ==> X = R / A (/A means inverse of matrix A or A^-1)

Matrix<3, 3> M = {
  pointA.x * pointA.x,   pointA.x,  1,
  pointB.x * pointB.x,   pointB.x,  1,
  pointC.x * pointC.x,   pointC.x,  1,
};

Matrix<3, 1> R = {
  pointA.y,
  pointB.y,
  pointC.y
};

void setup() {
  Serial.begin(115200);

  Matrix<3, 1> X = M.Inverse() * R;

  // printing the equation with no digits after the decimal dot for a,b and c
  // as I know it works with integral values but of course you would need
  // to use the full floating point value in reality

  Serial.print("Equation: y = ");

  if (X(0, 0) != 0) {
    Serial.print(X(0, 0), 0); // a
    Serial.print("x^2");
  }

  if (X(1, 0) != 0) {
    if (X(1, 0) > 0) Serial.write('+');
    Serial.print(X(1, 0), 0); // b
    Serial.write('x');
  }

  if (X(2, 0) != 0) {
    if (X(2, 0) > 0) Serial.write('+');
    Serial.print(X(2, 0), 0); // c
  }
  Serial.println();
}

void loop() {}

Serial Monitor (@ 115200 bauds) will show

[color=purple]
Equation: y = -1x^2+17x-30
[/color]

==> you can see we have the right coefficients: a=-1, b=17 and c=-30 and looking at the graph that curve does go through the 3 points

hope this helps