4-bits Binary Sum

Projects Programming
1

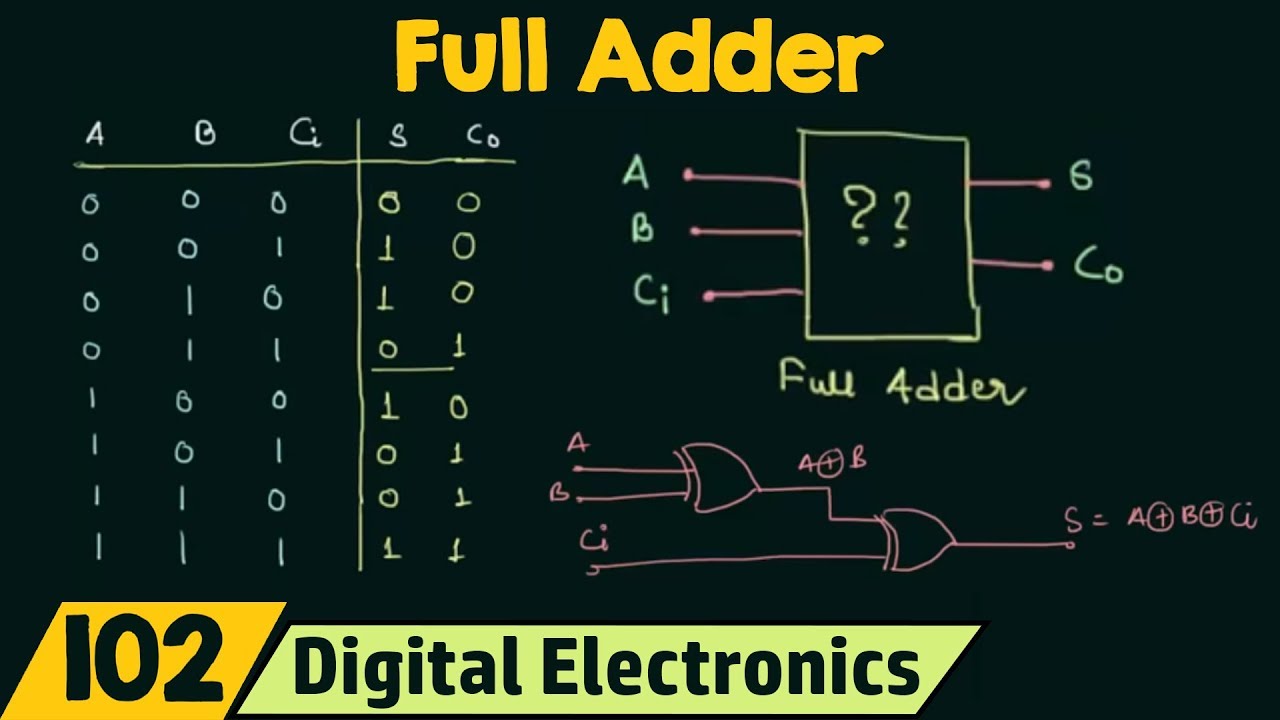
Hello, i'm working on this project in wich I had to make a calculator that added two 4 bit binary (or less) numbers, and they told me to use this code in class:

//Number 1
int A =12;
int B=11;
int C=10;
int D=9;

//Number 2
int E=8;
int F=7;
int G=6;
int H=5;

// Result
int Carry = 4;
int I =3;
int J=2;
int K=1;
int L=0; 

//boolean variables
bool a,b,c,d,e,f,g,h,i,j,k,l,carry1,carry2,carry3,carry4; 



void setup() {

 
  //Number 1
  pinMode(A, INPUT);
  pinMode(B, INPUT);
  pinMode(C, INPUT);
  pinMode(D, INPUT);
  
  //Number 2
  pinMode(E, INPUT);
  pinMode(F, INPUT);
  pinMode(G, INPUT);
  pinMode(H, INPUT);
  
  //Result
  pinMode(Carry, OUTPUT);
  pinMode(I, OUTPUT);
  pinMode(J, OUTPUT);
  pinMode(K, OUTPUT);
  pinMode(L, OUTPUT);
  
  
}


void loop() { 

  //Read input
  a = digitalRead(A);
  b = digitalRead(B);
  c = digitalRead(C);  
  d = digitalRead(D);
  e = digitalRead(E);
  f = digitalRead(F);
  g = digitalRead(G);
  h = digitalRead(H);
  
  //Process
  l = (!d && h) || (d && !h);
  carry1 = d&&h;
  
  k = (c && g && carry1) || (c && !g && !carry1) || (!c && g && !carry1) || (!c && !g && carry1);
  carry2 = (c && g && carry1) || (c && g && !carry1) || (c && !g && carry1) || (!c && g && carry1);
  
  j = (b && f && carry2) || (b && !f && !carry2) || (!b && f && !carry2) || (!b && !f && carry2);
  carry3 = (b && f && carry2) || (b && f && !carry2) || (b && !f && carry2) || (!b && f && carry2);
  
  
  i = (a && e && carry3) || (a && !e && !carry3) || (!a && e && !carry3) || (!a && !e && carry3);
  carry4 = (a && e && carry3) || (a && e && !carry3) || (a && !e && carry3) || (!a && e && carry3);
  
  
  
  //Bit 1
  if(l)
    digitalWrite(L, HIGH);
  else 
    digitalWrite(L,LOW);
    
  //Bit 2
  if(k)
    digitalWrite(K, HIGH);
  else 
    digitalWrite(K,LOW);
  
  //Bit 3
  if(j)
    digitalWrite(J, HIGH);
  else 
    digitalWrite(J,LOW);
  
  //Bit 4
  if(i)
    digitalWrite(I, HIGH);
  else 
    digitalWrite(I,LOW);
  
  //Carry
  if(carry4)
    digitalWrite(Carry, HIGH);
  else 
    digitalWrite(Carry,LOW);
 
  //Delay 
  delay(100);
}

Its supose to show the numbers being added up (modified with slide switchs) and the result as the series of LEDs (on and off) that makes up the number, but testing the code, it just doesnt work, it only turns up the LEDs of the result (except for the carry).
Also Im asked to see if I can change the use of slide switchs for buttons.

I'm not very good at python, and I really dont want to waste anyones time, but I wanted to see if someone could help. I would really want learn how to fix these and would appreciate any help.

2

Just now also they gave us these code which does uses the buttons, but it still doesnt work on the test:

const int binaryPins[] = {12, 11, 10, 9};
const int addPins[] = {8, 7, 6, 5};
const int resultPins[] = {4, 3, 2, 1, 0};

int binaryValue = 0;
int addValue = 0;

void setup() {
  for (int i = 0; i < 4; i++) {
    pinMode(binaryPins[i], INPUT_PULLUP);
    pinMode(addPins[i], INPUT_PULLUP);
    pinMode(resultPins[i], OUTPUT);
  }
  pinMode(resultPins[4], OUTPUT);
}

void loop() {
  binaryValue = 0;
  addValue = 0;

  for (int i = 0; i < 4; i++) {
    int binaryButtonState = digitalRead(binaryPins[i]);
    int addButtonState = digitalRead(addPins[i]);

    if (binaryButtonState == LOW) {
      binaryValue |= (1 << i); 

    if (addButtonState == LOW) {
      addValue |= (1 << i); 
    }
  }

  int result = binaryValue + addValue;

  for (int i = 0; i < 5; i++) {
    digitalWrite(resultPins[i], (result >> i) & 1);
  }
}
3

What does this mean exactly?

Pins 0 and 1 are usually reserved for communication. You might try using two of A0-A5 instead.

1 Like
4

I am not sure what "working" is, but the second code works.

5

This should be a fairly straightforward thing to do,
just search for "logic adder" on the internet....Then implement the logic using code.

6

what is "carry"? don't you say "binary sum"?

7

why

have 5 members?

8

No, in logic adders it's known as carry, as in carry from one adder to the next.

It includes the last carry out pin.

9

I'm not sure how to explain how logic adders work....But google "logic adder", you'll come up with results that'll explain it better then I can.

10

are we still on binary sum or normal? there is a little difference between + and & operation.
15 + 15 = 30, 15 & 15 = 15.

11

binary sum, also known as logic adder.

12

ok, then no carry is used. two 4bit sources and one 4bit output.

13

The carry output is used represent when someone adds 1111 to 1111....Instead of being 0000 it's 10000.

14 
const byte binaryPins[] = {11, 10, 9, 8};
const byte addPins[] = {7, 6, 5, 4};
const byte resultPins[] = {A3, A2, A1, A0};

void setup() {
  for (byte i = 0; i < 4; i++) {
    pinMode(binaryPins[i], INPUT_PULLUP);
    pinMode(addPins[i], INPUT_PULLUP);
    pinMode(resultPins[i], OUTPUT);
  }
}

void loop() {  for (int i = 0; i < 4; i++) {
  bool result = digitalRead(binaryPins[i]) & digitalRead(addPins[i]);
    digitalWrite(resultPins[i], result);
  }
}
15

wrong. if it normal adding ("+") it will resulting 11110.

1 Like
16

How do you represent 1111 + 1111 with that code?

17

you better use your own tip and go googling about.

18

Sorry....My fault, I didn't check it properly.

The point is you need the carry output....Otherwise 1110 + 0 is just the same as 1111 + 1111.

Without carry output.

1110 + 0000 = 1110
1111 + 1111 = 1110

With carry output.

1110 + 0000 = 0 1110
1111 + 1111 = 1 1110

19

Take a view here to gain the knowledge:

2 Likes
20

Thanks....I myself know full adders, half adders etc.

Unfortunately I'm not especially gifted with the skill of writing out in-depth explanations of things....I forgot about youtube too.

It also appears I haven't had enough sleep....I forgot how to add binary momentarily.