hi everyone
I'm using an arduino board with a monster shield to control a dc motor by using PWM
the relation between mechanical and electrical parts of the dc motor is defined as follows:
V=k*omega+(R/k)*tau
where V is voltage, k is motor constant, omega is angular velocity, R is the resistance of the motor and tau is the torque
if the dead-zone of the motor be equal to 0.1 N.m (torque) or 0.05 volts (Voltage) how I should add this dead-zone to the formulation?
As soon as someone writes something like that, 'as you know...", I immediately go on to the next thread, because I don't know...
Paul
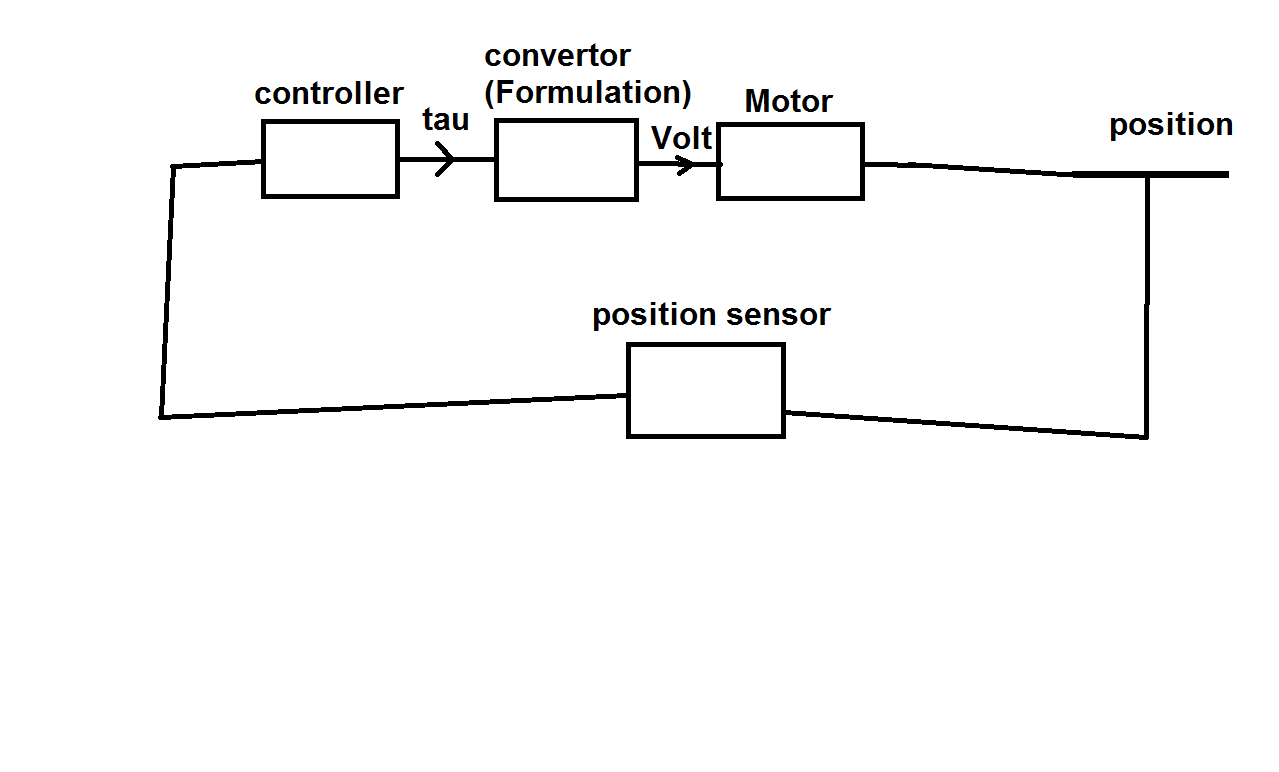
The formula isn't much use. If you want position control you need a feedback loop.
With an open loop and constant load you can simply guess. I say guess because it is faster by doing than trying to work out on paper because you could not be aware of all real elements of the system.
If your load is constant you can simply put a threshold.
ok I will edit my question
I have the feedback loop controller , but the input signal is torque and in the real experiment the torque must be convert to voltage and the relation is that formula and the dc motor has mechanical friction which assumed as dead-zone
Draw the block diagram.
The above sentence has no relationship to the block diagram you posted, in which the input signal (not shown) and feedback are position.
It would help if you spent a few moments describing the project on which you are actually working, possibly being "the real experiment".
The "dead zone" is the frictional loss, its a torque, not a voltage, and its sign depends on the sign of omega, so you'd split the equation into two versions depending on the sign of omega. Solid friction is fairly close to being constant (independent of speed), but this is
only a first-order approximation.
V = k * omega + R/k (tau + 0.1), omega > 0
= k * omega + R/k (tau - 0.1), omega < 0
(although I might have gotten my sings wrong!)
All units are S.I., for instance k is Vs/rad or Nm/A (which are the same thing !)
Note that R increases somewhat as the motor heats up, though you can simplify things
if you assume its constant. Friction (the 0.1Nm) also changes as the motor heats up,
usually falling considerably, and then there's viscous friction to consider (air drag and
bearing friction) which can be dominant at top speed.
thank you so much
This topic was automatically closed 120 days after the last reply. New replies are no longer allowed.