un résumé de ce poste qui est parti dans tous les sens est sur ce lien
un wiki suivant a été suppimé
https://digital-filter-atmega328-esp32.fandom.com/fr/wiki/Wiki_Filtre_numerique_digital_filter,_RII,_RIF,_atmega328,_ESP32
S’il y a de nombreux cours, livre sur internet sur les filtres numériques, il n’y a pas beaucoup d’exemples sur le net, ni de vulgarisation.
Voici quelques lien sur les filtres :
http://www.f-legrand.fr/scidoc/docimg/numerique/filtre/filtrenum/filtrenum.html
il y a sur ce lien, sur le filtrage avec Arduino
http://www.f-legrand.fr/scidoc/docimg/sciphys/arduino/filtrage2/filtrage2.html
Mais la vulgarisation n’est pas simple, car il y a de nombreuses méthodes pour déterminer les coefficients d’un filtre numérique à partir d’un gabarit désiré ou à partir d’un filtre analogique.
Evidemment, il y a des softs qui déterminent les coefficients assez facilement tel que :
Matlab filterBuilder pour Mathcad Plus avec des fonctions spécifiques
des soft en C Web Page Under Construction
Je n’ai pas réussi à faire fonctionner ce lien
jayduino - Arduino stuff written by me

Pas mieux avec ce lien ou il manque un help
http://t-filter.engineerjs.com/

Or, le traitement numérique est crucial pour isoler un signal du bruit, avoir des valeurs moyennes mais en gardant une certaine dynamique d’un capteur…..
Mais, les résultats du filtre vont dépendre de la précision du calcul, de la période d’échantillonnage, donc du temps de calculs du processeur et du compilateur.
Souvent, les étudiants apprennent l’étude des filtres avec Matlab qui peut travailler à des fréquences d’échantillonnages très grandes et avec des précisions de calculs à plus de 18 chiffres après la virgule.
Mais avec un Arduino nano, on peut facilement observer les limites du traitement numérique d’un petit processeur ?
Avec l’IDE d’Arduino, la déclaration en float, n’a que 7 chiffres significatifs par excès :
dont voici un exemple : 0.1234567 ou 1.123456 ou 12.345
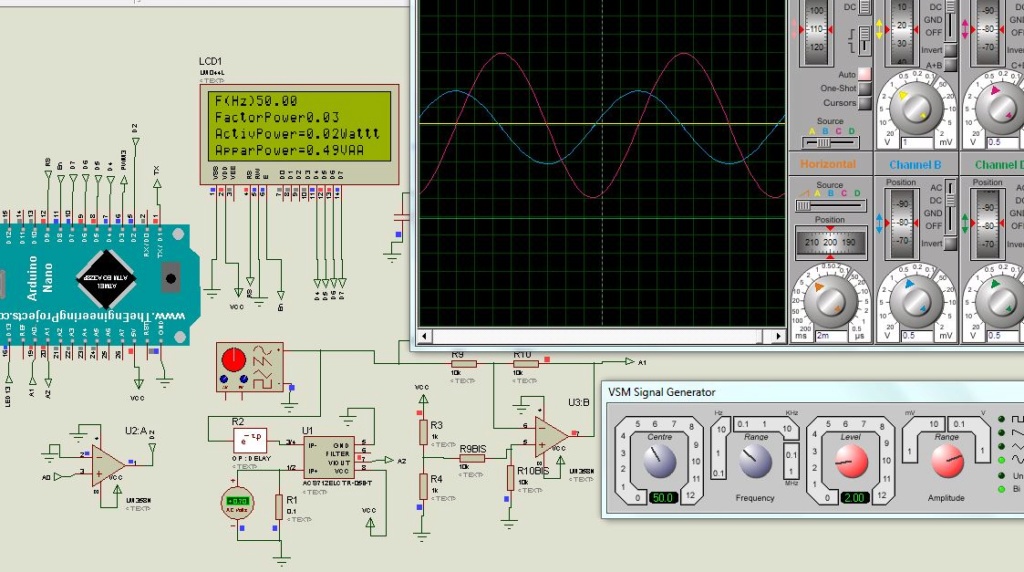
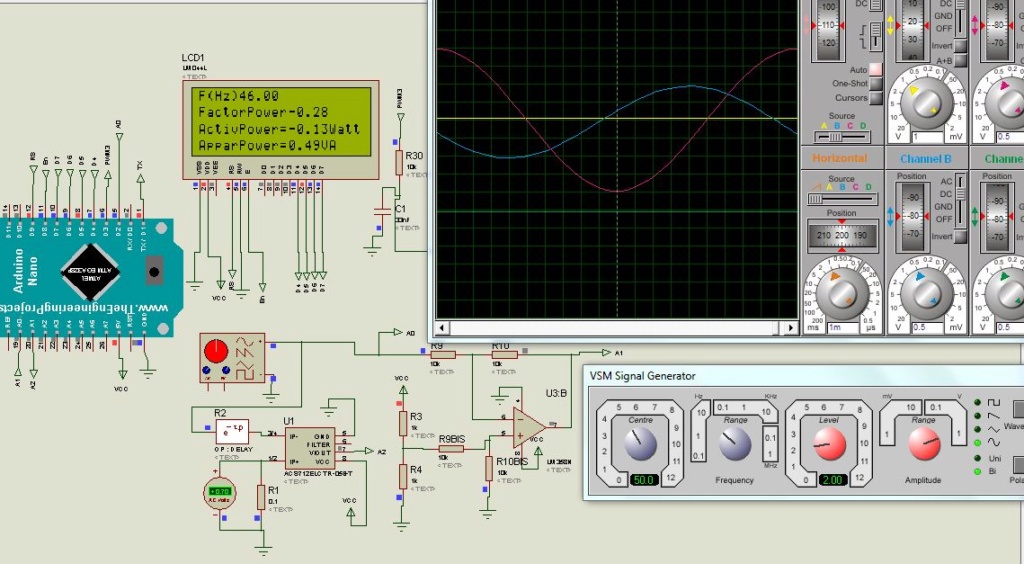
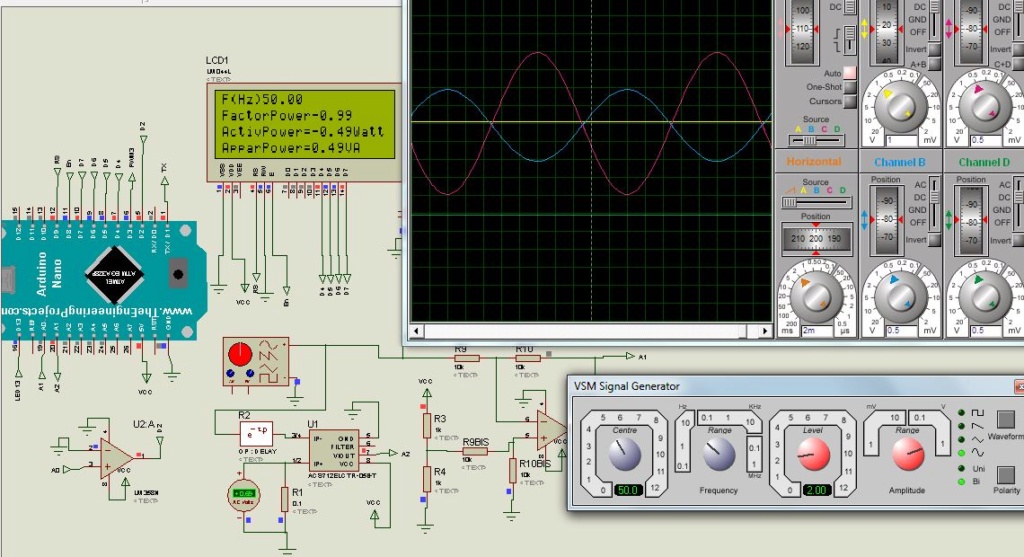
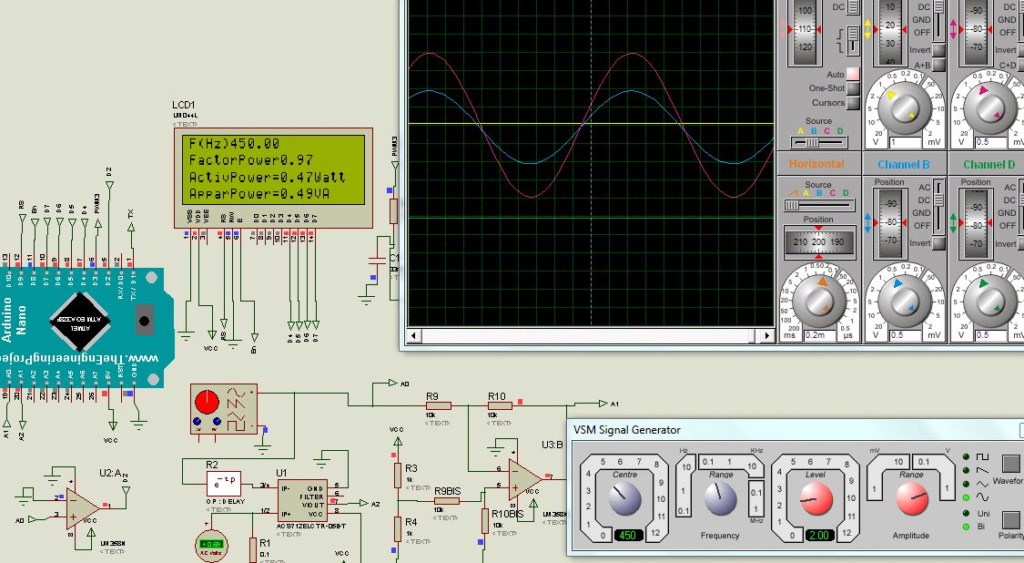
La base d’un programme sur les filtres numériques est une lecture d’un signal d’entrée analogique fournit par un GBF et une sortie qui peut être le terminal, le traceur série, ou une PWM. L’afficheur LCD n’est pas utile mais permet de debugger le programme parfois.
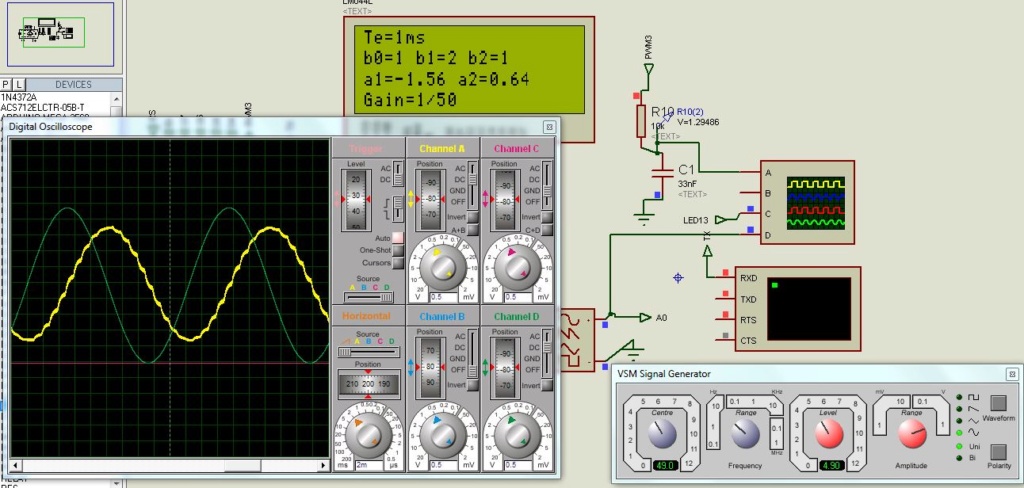
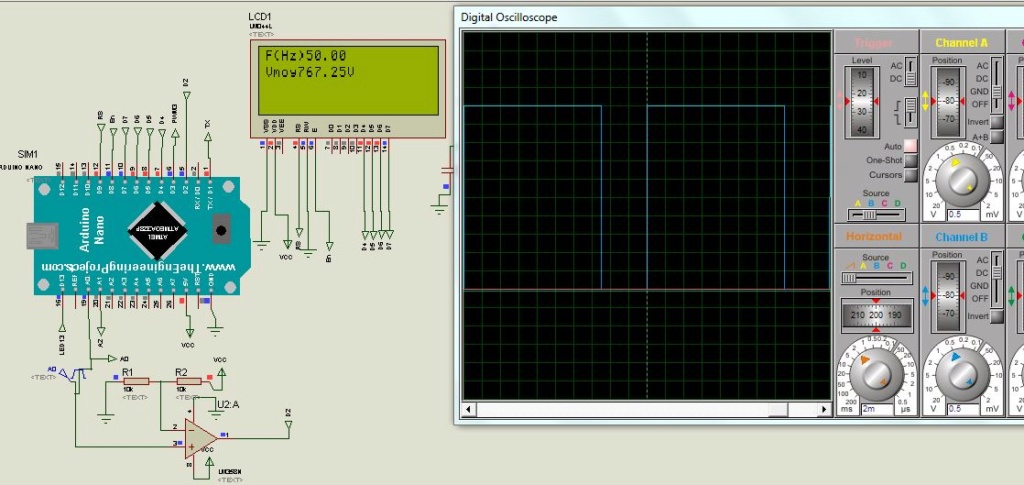
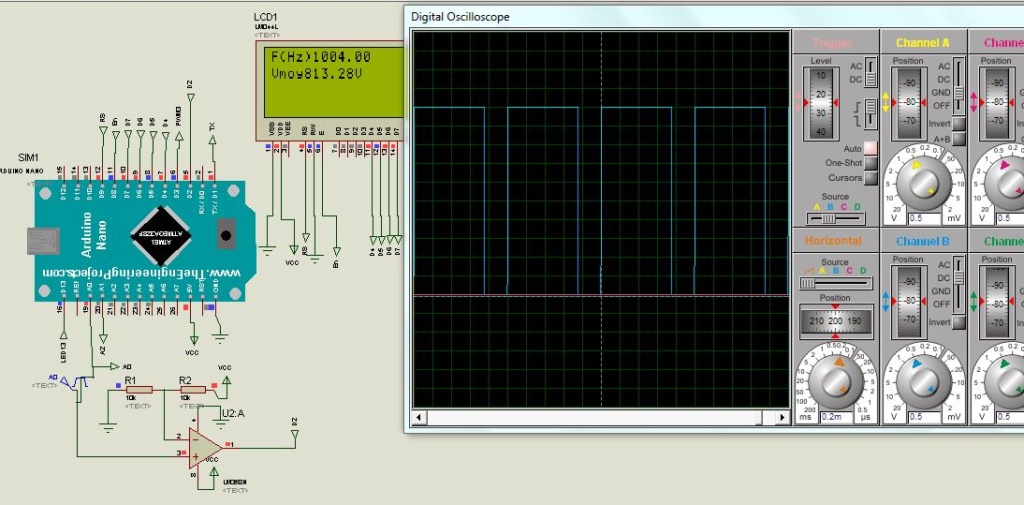
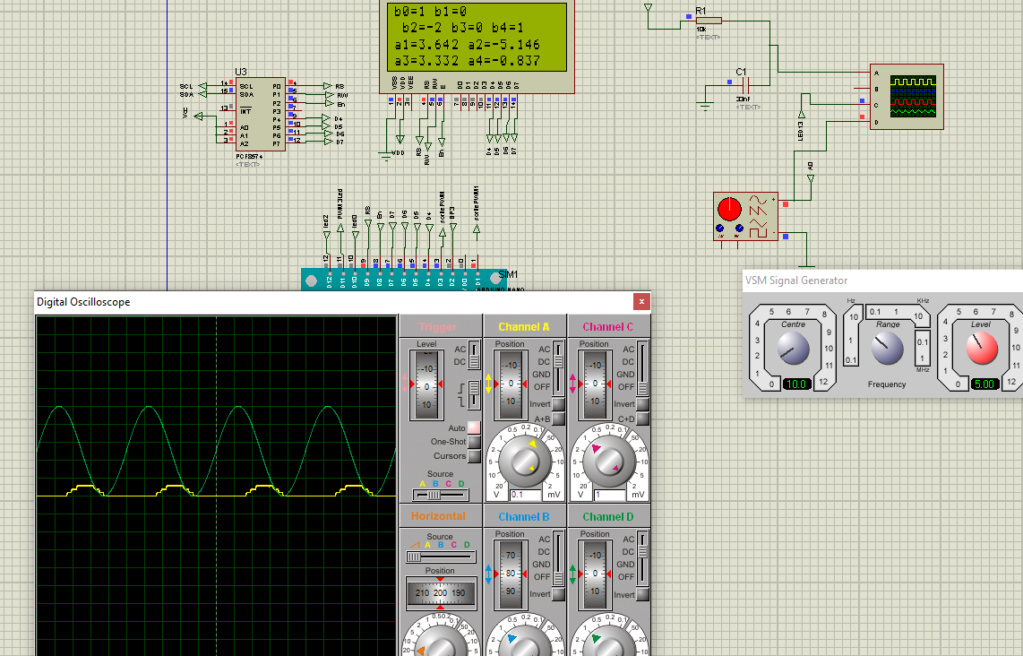
Un Arduino nano sera utilisé avec une PWM avec une fréquence de 32kHz bien supérieure à la période d’échantillonnage fixé arbitrairement à 1ms, et un RC de (10kohms et une capacité de 33nF) donc une fréquence de coupure de 482Hz atténuera l'ondulation du signal carré de la PWM comme on peut l’observer sur la figure suivante :
Le programme de base avec un gain unitaire est le suivant avec Te=1ms dans une routine interruption :
Ce programme de base dure 150microseconde, donc cela laisse du temps à faire du traitement numérique dans cette routine.
#include <LiquidCrystal.h>
#include <SoftwareSerial.h>
#include <TimerOne.h>
#define PWM3 3 // timer2
#define LED13 13
LiquidCrystal lcd(9, 8, 4, 5, 6, 7); // LiquidCrystal lcd(rs, en, d4, d5, d6, d7);
// Configuration des variables
unsigned int temps=0;
float entree=0;
float entree1=0;
float entree2=0;
float sortie=0;
float sortie1=0;
float sortie2=0;
float out=0;
const float b1 =2;
const float b2 =1;
const float a1 =-1.911;
const float a2 =0.915;
const float gain =1000;
void setup() {
pinMode(LED13, OUTPUT);
pinMode(PWM3,OUTPUT);
Timer1.initialize(1000); // initialize timer1, and set a 0,1 second period => 100 000 pour 0.01s 10 000
Timer1.attachInterrupt(callback); // attaches callback() as a timer overflow interrupt
lcd.begin(16, 2); //modifier pour un afficheur 20x4
Serial.begin(9600);
TCCR2B = (TCCR2B & 0b11111000) | 0x01; //pin 3 32khz http://playground.arduino.cc/Main/TimerPWMCheatsheet
}
// Interruptions tous les 1ms fait par le timer1***********************************
void callback() {
digitalWrite(LED13,HIGH); //permet de mesurer à l'oscillo, le temps du calcul du filtre et le temps de la routine d'interruption
entree=analogRead(A0); //convertisseur 10 bits sous 5V
/* ---- exemple filtre passe pas Butterwoth pour fc=10hz, fechantillon=1000Hz------
entree2=entree1; //entree(n-2)
entree1=entree; //entree(n-1)
sortie2=sortie1; //sortie(n-2)
sortie1=sortie; //sortie(n-1)
//sortie=entree+entree1*b1+entree2*b2+entree3*b3-sortie1*a1-sortie2*a2-sortie3*a3 ; //filtre passe pas recursif ordre 3
//sortie=(entree+entree1*b1+entree2*b2-sortie1*a1-sortie2*a2) ; //filtre passe pas recursif ordre 2
*/
sortie=entree/4 ; //mise à l'echelle 10 bits en entrée et 8 bits en sortie
//out = map(out, 0, 1023, 0, 255); //mise à l'echelle 10 bits en entrée et 8 bits en sortie
if ( sortie>254) {sortie=254;}
analogWrite(PWM3,sortie); //
digitalWrite(LED13,LOW);
/* creation du fichier CSV traçage dans Excel
Serial.print(entree); Serial.print(";"); Serial.print("\t"); //entrée
Serial.print(sortie); Serial.print("\t"); Serial.println(";"); //mise à la ligne dans le terminal
*/
}//fin routine
///////////////////////////////////////////// Boucle correspondant à la fonction main
void loop() {
lcd.setCursor(0,0);
lcd.print("filtre numerique ");
lcd.setCursor(0,1);
lcd.print("IUT GEIIsoissons ");
} // fin loop
Le fichier de simulation ISIS peut être téléchargé sur ce lien
Attention la PWM demande beaucoup de ressource de calcul pour ISIS par le PC, donc souvent il vaut mieux travailler en reel qu’en simulation.

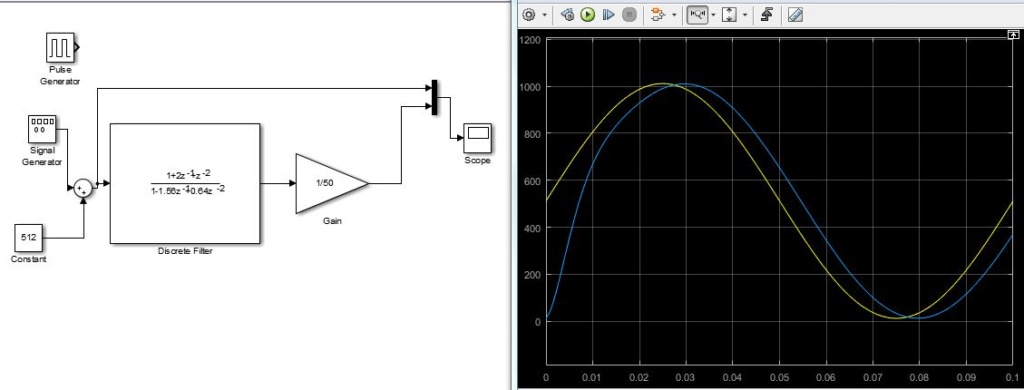
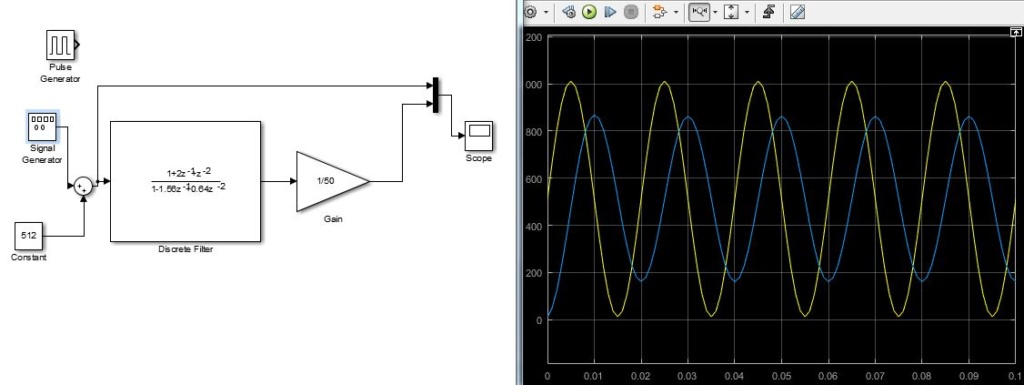
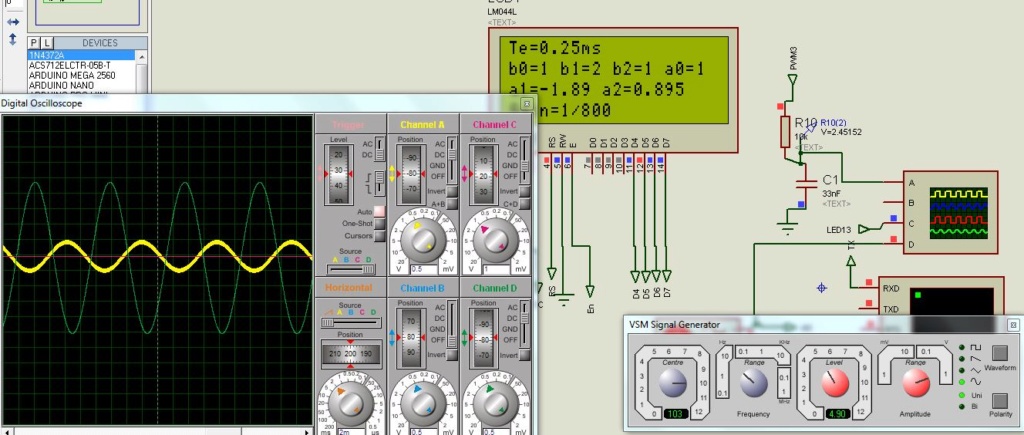
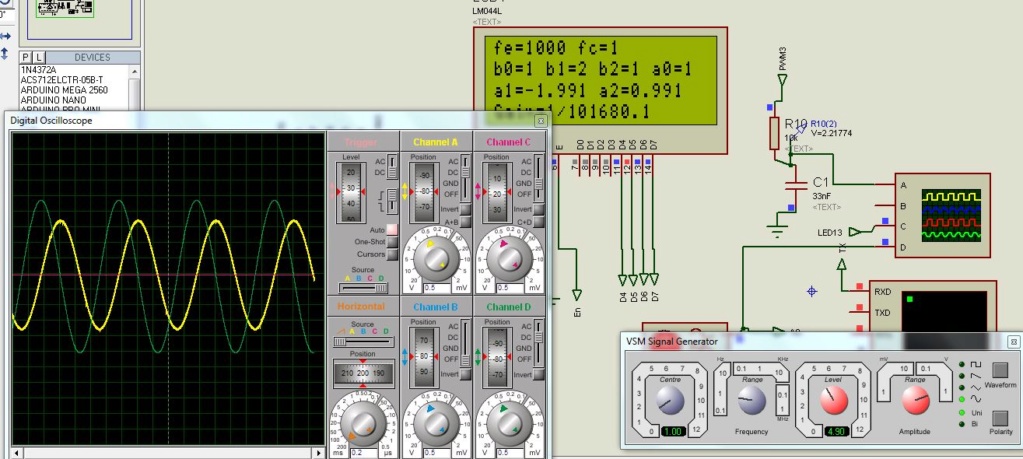
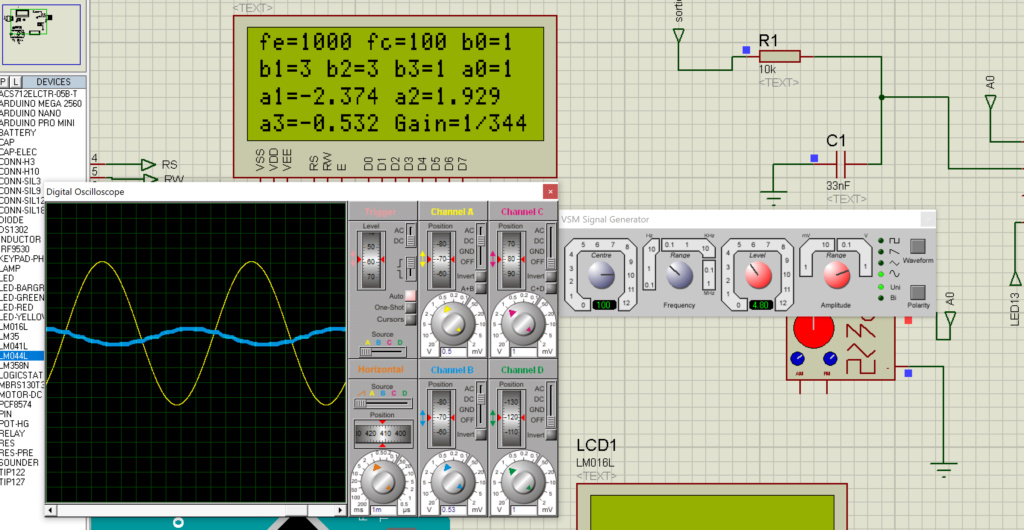
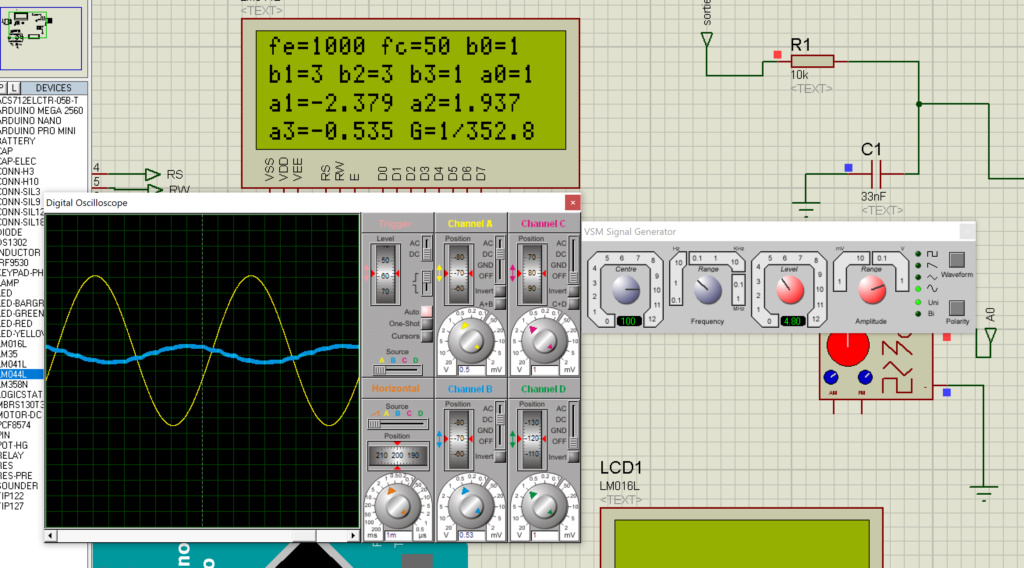
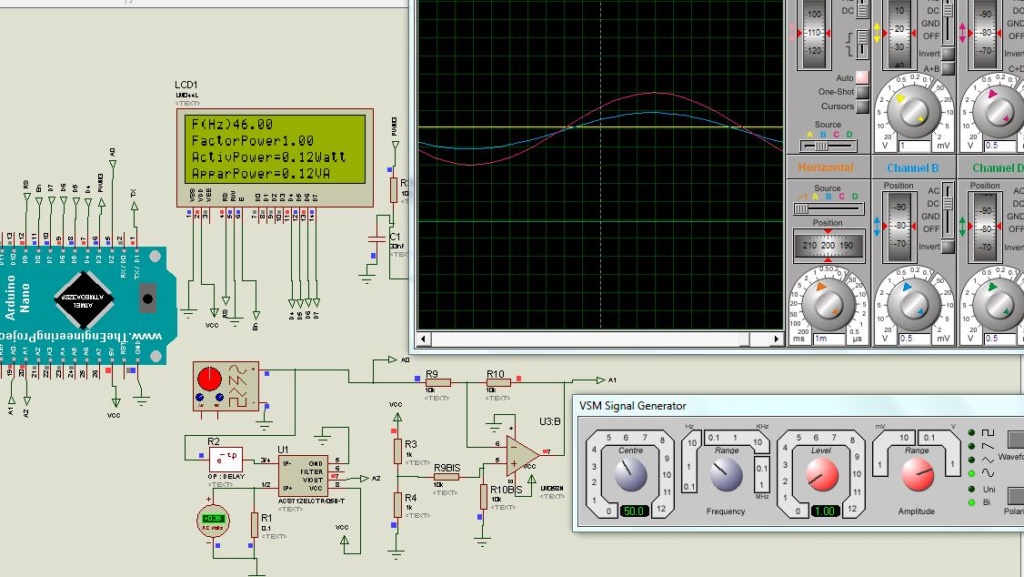
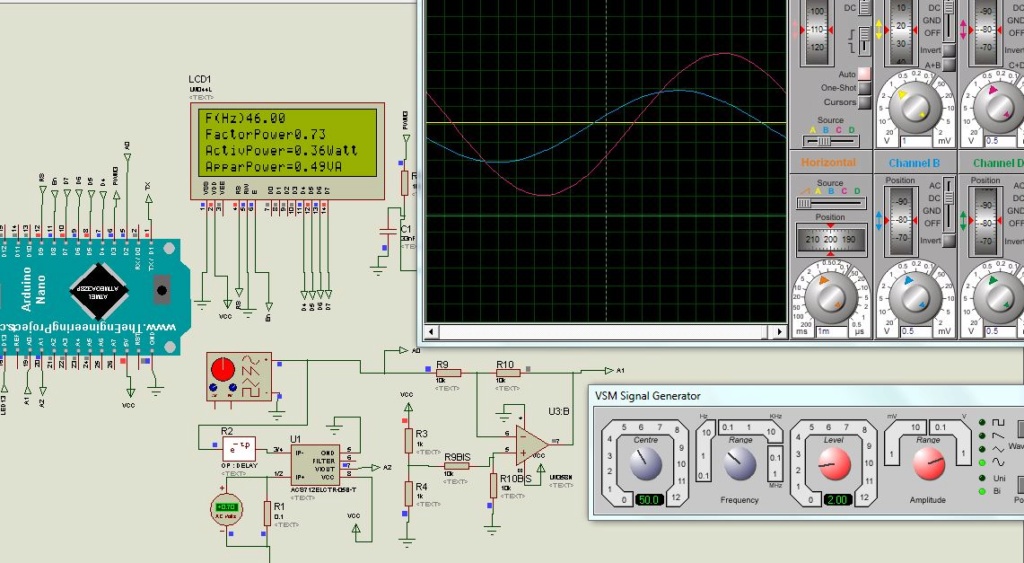
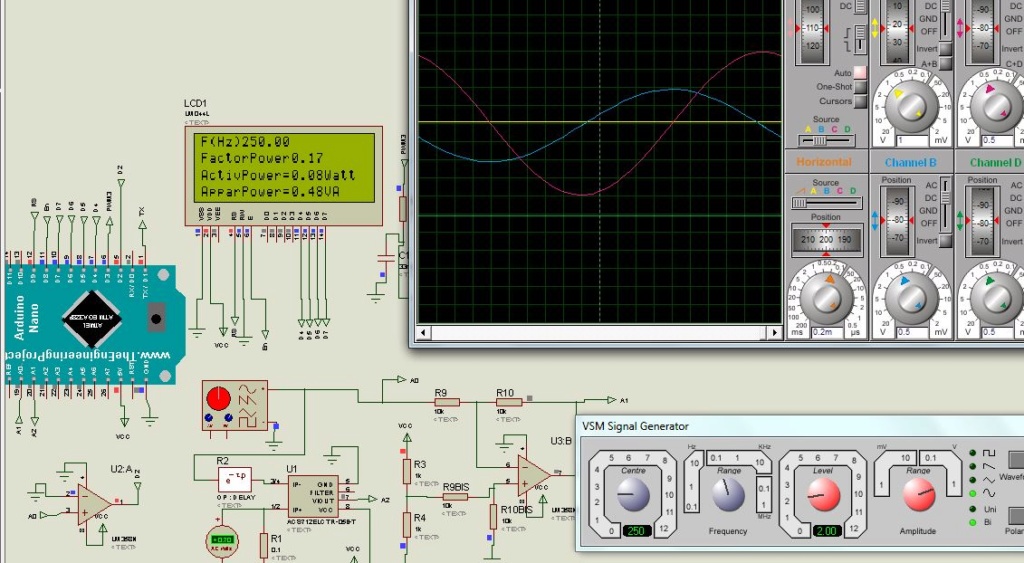
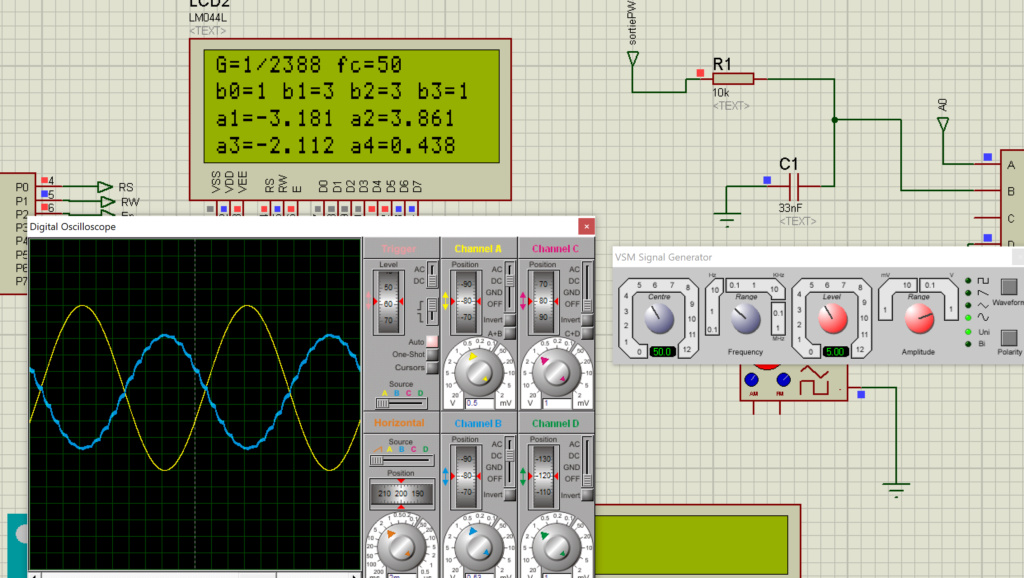
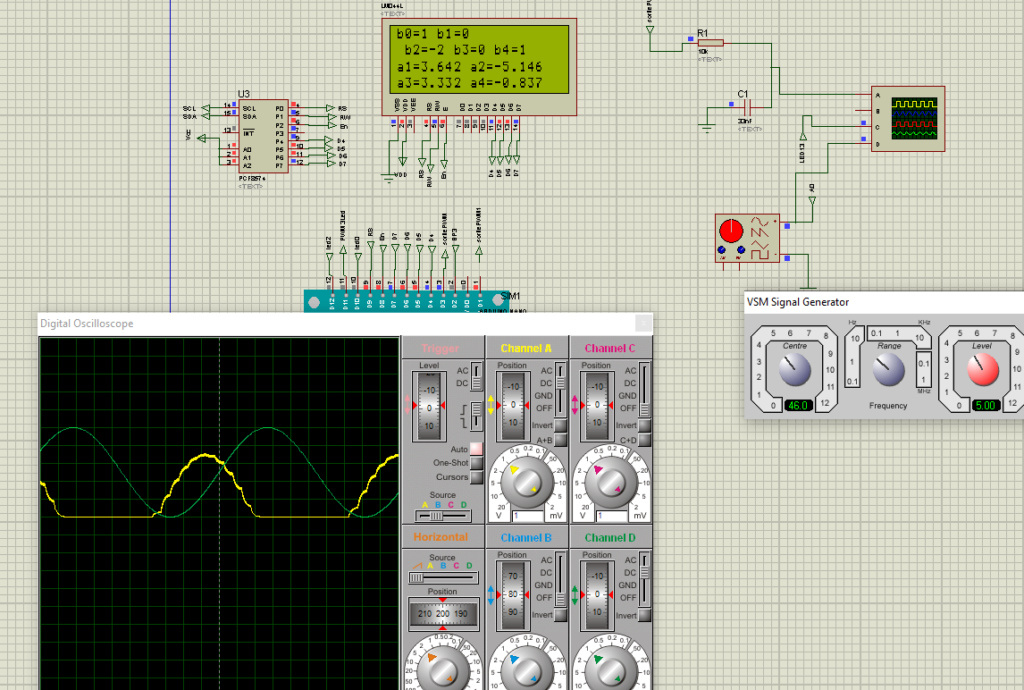
Avec une période d’échantillonnage de 1kHz, un signal sinusoïdale de 200Hz a été mis, on peut observer les différences de sorties à cause qu’il n’y a que 5 échantillons de mesure de ce signal.

Photo du banc en reel à venir et
Sommaire
Voici la définition des filtres numeriques
il existe 2 types de filtres
• RIF : Filtre à réponse impulsionnelle finie dépendant que de l’entrée et peu seulement converger.
RII : (Filtre à réponse impulsionnelle infinie) dépendant de l’entrée et d’ancienne et sortie et peut diverger
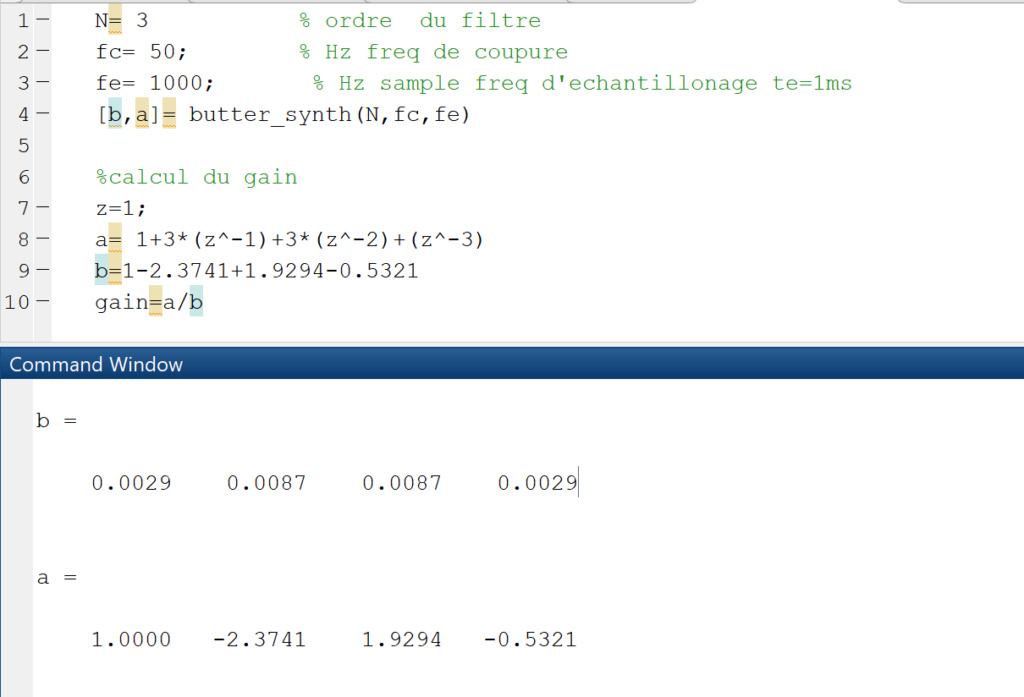
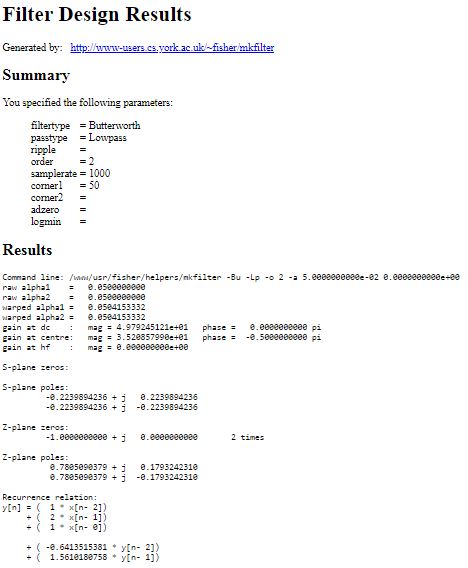
Dans un premier temps, Nous allons présenter comment on troupe les coefficients de filtres récursif RII.
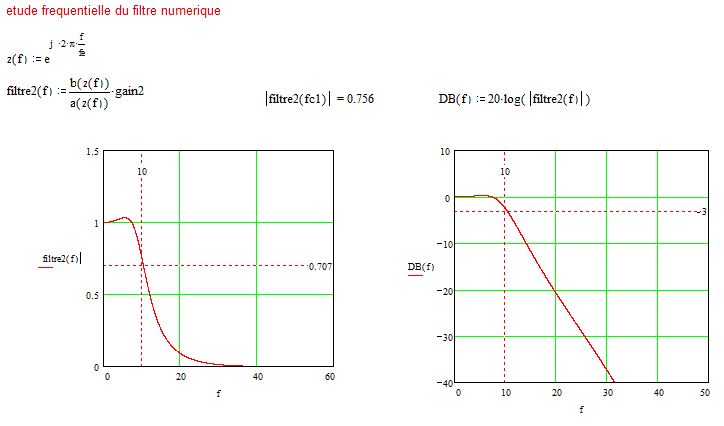
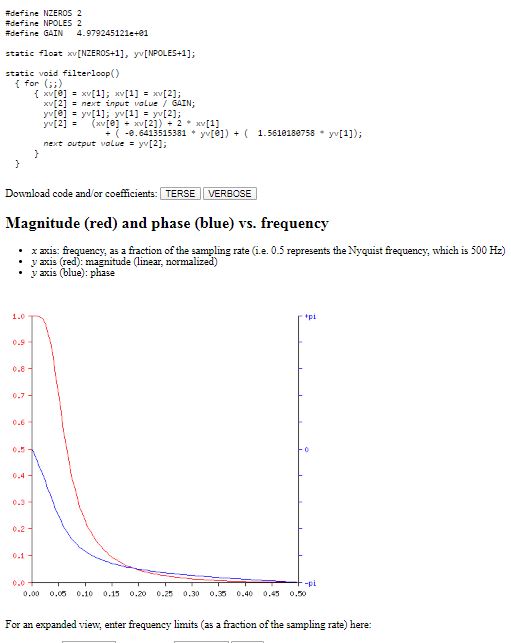
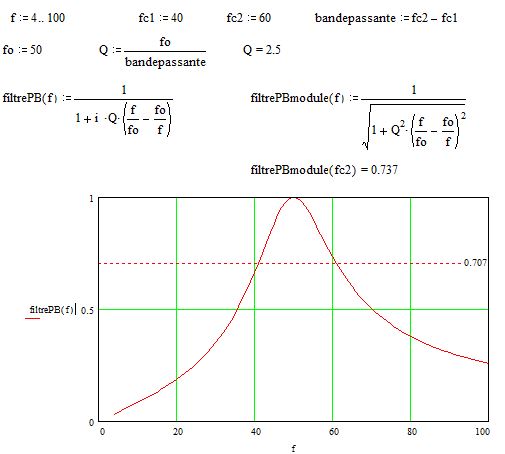
Puis, la courbe d’atténuation théorique sera tracé, et 5 valeurs en réelles seront prix pour vérifier la théorie.
- Etude filtre passe bas de premier ordre RC,
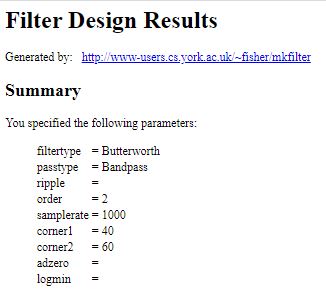
En mode sinusoïdale et en mode temporel avec un signal carré. - Filtre butterworth passe bas, d’ordre 1
Filtre de Butterworth — Wikipédia
En mode sinusoïdale et en mode temporel avec un signal carré. - Filtre butterworth passe bas, d’ordre 2
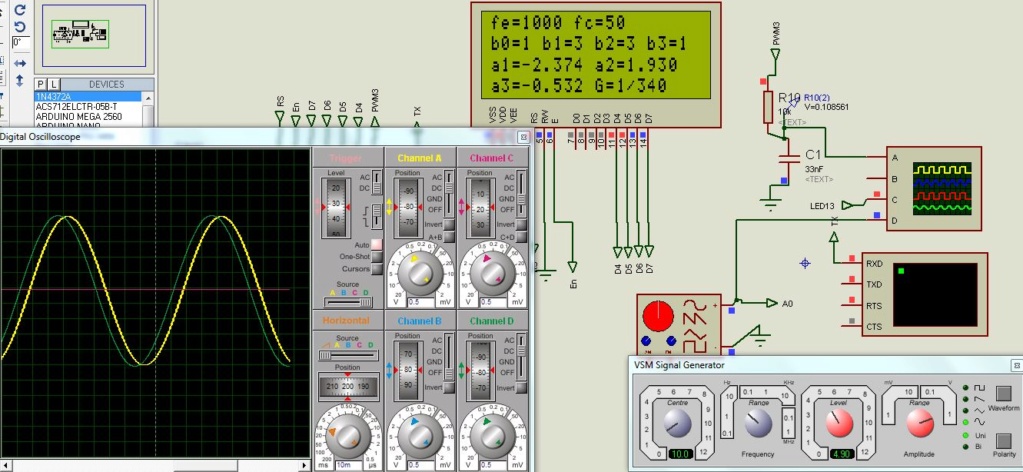
- Filtre butterworth passe bas, d’ordre 3
Dans un deuxième temps, des Filtres numériques moyenneur RIF seront presentés
https://www.f-legrand.fr/scidoc/docimg/numerique/filtre/rif/rif.html
http://herve.boeglen.free.fr/Tsignal/chapitre3/chapitre3.htm
De nombreux essais vont etre realisés sur ce sujet pour expliquer le filtrage numerique par des etudiants.
Ce qui sera peut-être plus explicite qu’un spécialiste du domaine ou que des bibliothèques ou l’on ne connait pas les tenants et les aboutissants
https://playground.arduino.cc/Code/Filters/