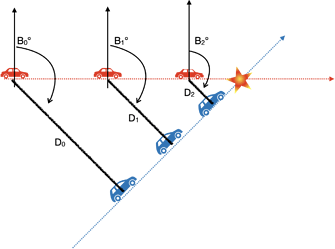
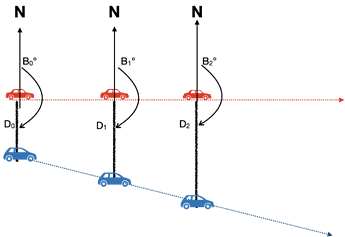
Really the maths are not that complicated if you go for bearing and distance and you receive the position at 1Hz.
Any arduino can handle that.
if you want to verify the performance, run this code on your target architecture
#include <Time.h>
// let's imagine this is the structure that we broadcast for each vehicle
struct __attribute__((packed)) t_VehicleInfo {
uint32_t ID; // vehicle ID
double lat; // current latitude
double lng; // current longitude
time_t when; // when the fix was taken (UTC)
};
// see https://github.com/mikalhart/TinyGPSPlus or http://arduiniana.org/libraries/tinygpsplus/
// functions taken out of the TinyGPS++ library
// returns distance in meters between two positions, both specified
// as signed decimal-degrees latitude and longitude. Uses great-circle
// distance computation for hypothetical sphere of radius 6372795 meters.
// Because Earth is no exact sphere, rounding errors may be up to 0.5%.
// Courtesy of Maarten Lamers
double distanceBetween(double lat1, double long1, double lat2, double long2) {
double delta = radians(long1 - long2);
double sdlong = sin(delta);
double cdlong = cos(delta);
lat1 = radians(lat1);
lat2 = radians(lat2);
double slat1 = sin(lat1);
double clat1 = cos(lat1);
double slat2 = sin(lat2);
double clat2 = cos(lat2);
delta = (clat1 * slat2) - (slat1 * clat2 * cdlong);
delta = sq(delta);
delta += sq(clat2 * sdlong);
delta = sqrt(delta);
double denom = (slat1 * slat2) + (clat1 * clat2 * cdlong);
delta = atan2(delta, denom);
return delta * 6372795;
}
// returns course in degrees (North=0, West=270) from position 1 to position 2,
// both specified as signed decimal-degrees latitude and longitude.
// Because Earth is no exact sphere, calculated course may be off by a tiny fraction.
// Courtesy of Maarten Lamers
double courseTo(double lat1, double long1, double lat2, double long2) {
double dlon = radians(long2 - long1);
lat1 = radians(lat1);
lat2 = radians(lat2);
double a1 = sin(dlon) * cos(lat2);
double a2 = sin(lat1) * cos(lat2) * cos(dlon);
a2 = cos(lat1) * sin(lat2) - a2;
a2 = atan2(a1, a2);
if (a2 < 0.0) a2 += TWO_PI;
return degrees(a2);
}
t_VehicleInfo vehicle1 = {1, 49.239038, -2.101748, 0};
t_VehicleInfo vehicle2 = {2, 49.239058, -2.102092, 0};
void setup() {
Serial.begin(115200); Serial.println();
}
void loop() {
uint32_t t0 = micros();
double distance = distanceBetween(vehicle1.lat, vehicle1.lng, vehicle2.lat, vehicle2.lng);
double course = courseTo(vehicle1.lat, vehicle1.lng, vehicle2.lat, vehicle2.lng);
uint32_t deltaT = micros() - t0;
Serial.print(F("Course : ")); Serial.print(course, 2); Serial.println(F("°"));
Serial.print(F("Distance : ")); Serial.print(distance, 2); Serial.println(F(" m"));
Serial.print(F("Compute time : ")); Serial.print(deltaT); Serial.println(F(" µs"));
Serial.println(F("-------------"));
vehicle2.lat += ((double) random(-100, 100)) / 100000.0; // create a small variation
vehicle2.lng += ((double) random(-100, 100)) / 100000.0; // create a small variation
delay(1000); // update at 1Hz
}
I would expect each evaluation to take less than 1.5ms on an Arduino Nano or UNO and probably ten time faster (less than 150µs) on an ESP32.
and because the 2 functions we call in sequence have some maths in common, you could optimise that by having only one function that returns both the course and the distance
Taking a board with 2 or more serial ports will make listening to the GPS more robust than a software serial solution, that's the only reason why I would move away from Uno or Nano (in prototyping stage of course)