Running SOLAr position algorithm

Projects Programming
1

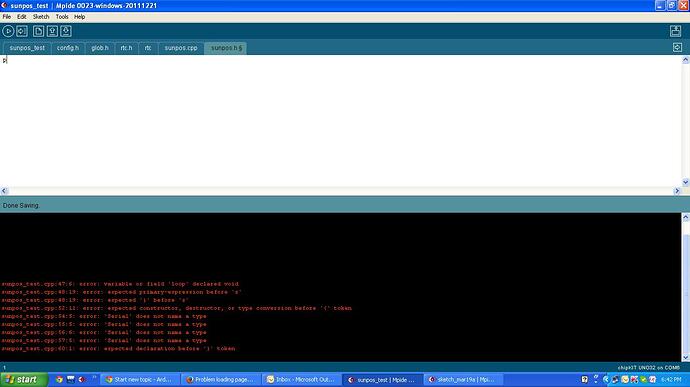
I wanted to run below code on Arduino platform. I am getting below error.

void loop{
  cSunCoordinates s;
    cTime t = {yy, mm, dd,h, m,s};
    cLocation l = {latitude,longitude};
  
    sunpos(t, l, &s);

    Serial.print("Zenith:");
    Serial.println(s.dZenithAngle);
     Serial.print("Azimuth:");
    Serial.println(s.dAzimuth);
    
   
}

Sunpos.cpp

#include "sunpos.h"
#include <math.h>

void sunpos(cTime udtTime,cLocation udtLocation, cSunCoordinates *udtSunCoordinates)
{
	// Main variables
	double dElapsedJulianDays;
	double dDecimalHours;
	double dEclipticLongitude;
	double dEclipticObliquity;
	double dRightAscension;
	double dDeclination;

	// Auxiliary variables
	double dY;
	double dX;

	// Calculate difference in days between the current Julian Day 
	// and JD 2451545.0, which is noon 1 January 2000 Universal Time
	{
		double dJulianDate;
		long int liAux1;
		long int liAux2;
		// Calculate time of the day in UT decimal hours
		dDecimalHours = udtTime.dHours + (udtTime.dMinutes 
			+ udtTime.dSeconds / 60.0 ) / 60.0;
		// Calculate current Julian Day
		liAux1 =(udtTime.iMonth-14)/12;
		liAux2=(1461*(udtTime.iYear + 4800 + liAux1))/4 + (367*(udtTime.iMonth 
			- 2-12*liAux1))/12- (3*((udtTime.iYear + 4900 
		+ liAux1)/100))/4+udtTime.iDay-32075;
		dJulianDate=(double)(liAux2)-0.5+dDecimalHours/24.0;
		// Calculate difference between current Julian Day and JD 2451545.0 
		dElapsedJulianDays = dJulianDate-2451545.0;
	}

	// Calculate ecliptic coordinates (ecliptic longitude and obliquity of the 
	// ecliptic in radians but without limiting the angle to be less than 2*Pi 
	// (i.e., the result may be greater than 2*Pi)
	{
		double dMeanLongitude;
		double dMeanAnomaly;
		double dOmega;
		dOmega=2.1429-0.0010394594*dElapsedJulianDays;
		dMeanLongitude = 4.8950630+ 0.017202791698*dElapsedJulianDays; // Radians
		dMeanAnomaly = 6.2400600+ 0.0172019699*dElapsedJulianDays;
		dEclipticLongitude = dMeanLongitude + 0.03341607*sin( dMeanAnomaly ) 
			+ 0.00034894*sin( 2*dMeanAnomaly )-0.0001134
			-0.0000203*sin(dOmega);
		dEclipticObliquity = 0.4090928 - 6.2140e-9*dElapsedJulianDays
			+0.0000396*cos(dOmega);
	}

	// Calculate celestial coordinates ( right ascension and declination ) in radians 
	// but without limiting the angle to be less than 2*Pi (i.e., the result may be 
	// greater than 2*Pi)
	{
		double dSin_EclipticLongitude;
		dSin_EclipticLongitude= sin( dEclipticLongitude );
		dY = cos( dEclipticObliquity ) * dSin_EclipticLongitude;
		dX = cos( dEclipticLongitude );
		dRightAscension = atan2( dY,dX );
		if( dRightAscension < 0.0 ) dRightAscension = dRightAscension + twopi;
		dDeclination = asin( sin( dEclipticObliquity )*dSin_EclipticLongitude );
	}

	// Calculate local coordinates ( azimuth and zenith angle ) in degrees
	{
		double dGreenwichMeanSiderealTime;
		double dLocalMeanSiderealTime;
		double dLatitudeInRadians;
		double dHourAngle;
		double dCos_Latitude;
		double dSin_Latitude;
		double dCos_HourAngle;
		double dParallax;
		dGreenwichMeanSiderealTime = 6.6974243242 + 
			0.0657098283*dElapsedJulianDays 
			+ dDecimalHours;
		dLocalMeanSiderealTime = (dGreenwichMeanSiderealTime*15 
			+ udtLocation.dLongitude)*rad;
		dHourAngle = dLocalMeanSiderealTime - dRightAscension;
		dLatitudeInRadians = udtLocation.dLatitude*rad;
		dCos_Latitude = cos( dLatitudeInRadians );
		dSin_Latitude = sin( dLatitudeInRadians );
		dCos_HourAngle= cos( dHourAngle );
		udtSunCoordinates->dZenithAngle = (acos( dCos_Latitude*dCos_HourAngle
			*cos(dDeclination) + sin( dDeclination )*dSin_Latitude));
		dY = -sin( dHourAngle );
		dX = tan( dDeclination )*dCos_Latitude - dSin_Latitude*dCos_HourAngle;
		udtSunCoordinates->dAzimuth = atan2( dY, dX );
		if ( udtSunCoordinates->dAzimuth < 0.0 ) 
			udtSunCoordinates->dAzimuth = udtSunCoordinates->dAzimuth + twopi;
		udtSunCoordinates->dAzimuth = udtSunCoordinates->dAzimuth/rad;
		// Parallax Correction
		dParallax=(dEarthMeanRadius/dAstronomicalUnit)
			*sin(udtSunCoordinates->dZenithAngle);
		udtSunCoordinates->dZenithAngle=(udtSunCoordinates->dZenithAngle 
			+ dParallax)/rad;
	}
}

sunpos.h

#ifndef __SUNPOS_H
#define __SUNPOS_H


// Declaration of some constants 
#define pi    3.14159265358979323846
#define twopi (2*pi)
#define rad   (pi/180)
#define dEarthMeanRadius     6371.01	// In km
#define dAstronomicalUnit    149597890	// In km

struct cTime
{
	int iYear;
	int iMonth;
	int iDay;
	double dHours;
	double dMinutes;
	double dSeconds;
};

struct cLocation
{
	double dLongitude;
	double dLatitude;
};

struct cSunCoordinates
{
	double dZenithAngle;
	double dAzimuth;
};

void sunpos(cTime udtTime, cLocation udtLocation, cSunCoordinates *udtSunCoordinates);

#endif

error.JPG
error.JPG1366×768 72.7 KB

2 
void loop{

Should be:

void loop(){
3

That sun position algorithm appears to rely on 64 bit double precision floating point math, which the Arduino does not support (double is treated the same as float). At the very least the accuracy will be reduced and the algorithm might fail altogether. Be sure to check the output with some known test cases!

4

Be sure to check the output with some known test cases!

Set the controls for the heart of the sun.

5

AWOL:

Be sure to check the output with some known test cases!

Set the controls for the heart of the sun.

+1. :grin:

None of that math above is required. I do full solar modelling with corrections for Kepler's Laws and so on without having a clue exactly how far away, other than knowing the deviation from the means is +/- 3% and the closest date is early January.

The sun is a giant orange ball and it moves REALLY REALLY FAST. High precision is NOT required!

6

The sun is a giant orange ball and it moves REALLY REALLY FAST.

Actually, it doesn't. It moves relatively slowly. It is the earth that is rotating and revolving that causes the APPARENT motion of the sun.

7

High precision is NOT required!

I know this and you know this, but this particular user and his/her sock-puppets don't want to listen, and haven't been listening for quite some time.
It's getting tedious.

8

PaulS:

The sun is a giant orange ball and it moves REALLY REALLY FAST.

Actually, it doesn't. It moves relatively slowly. It is the earth that is rotating and revolving that causes the APPARENT motion of the sun.

Relative to what though? It's pretty fast moving relative to its centre of orbit. XD

9

Here I am running Nrel c code on Arduino mega and Chipkit UNO32 Using MPIDE 0023 IDE .
Here i have attached code and expected output from Nrel. How to get Double Precision floating point values. I am using Windows XP , MPide V0023 .
In my code ,spa.cpp and spa_h changed DOuble to float. Still i am getting same result. Let me know how to solve this issue.

nrel-visualstudio.JPG
nrel-visualstudio.JPG970×610 32.7 KB

spa_tester.rar (9.99 KB)

Nrel-Ardunio_chipkit.JPG

10

Where is the latest (and full) code your playing with?
I knocked up this sketch...

#include "sunpos.h"

int yy = 2014;
int mm = 3;
int dd =21;
float h = 13.0;
float m = 0.0;
float s = 0.0;
float latitude = 52.6028;
float longitude = 0.3777;

cSunCoordinates ss;

void setup(){
  Serial.begin(115200);
}

void loop(){
  cLocation l = {latitude,longitude};
  for (h = 0; h < 24; h++){
    cTime t = {yy, mm, dd, h, m, s};
    
    sunpos(t, l, &ss);
    
    Serial.print("Hour: ");
    Serial.print(h);
    Serial.print("\tZenith: ");
    Serial.print(ss.dZenithAngle);
    Serial.print("\tAzimuth: ");
    Serial.println(ss.dAzimuth);
  }
  while(1){};
}

And it prints this...

Hour: 0.00	Zenith: 129.22	Azimuth: 89.54
Hour: 1.00	Zenith: 114.22	Azimuth: 89.70
Hour: 2.00	Zenith: 99.22	Azimuth: 89.82
Hour: 3.00	Zenith: 84.22	Azimuth: 89.92
Hour: 4.00	Zenith: 69.20	Azimuth: 89.91
Hour: 5.00	Zenith: 54.20	Azimuth: 90.01
Hour: 6.00	Zenith: 39.20	Azimuth: 90.12
Hour: 7.00	Zenith: 24.20	Azimuth: 90.31
Hour: 8.00	Zenith: 9.20	Azimuth: 90.98
Hour: 9.00	Zenith: 5.82	Azimuth: 269.40
Hour: 10.00	Zenith: 20.82	Azimuth: 269.89
Hour: 11.00	Zenith: 35.82	Azimuth: 270.01
Hour: 12.00	Zenith: 50.82	Azimuth: 270.10
Hour: 13.00	Zenith: 65.82	Azimuth: 270.18
Hour: 14.00	Zenith: 80.82	Azimuth: 270.26
Hour: 15.00	Zenith: 95.82	Azimuth: 270.36
Hour: 16.00	Zenith: 110.83	Azimuth: 270.59
Hour: 17.00	Zenith: 125.83	Azimuth: 270.78
Hour: 18.00	Zenith: 140.83	Azimuth: 271.12
Hour: 19.00	Zenith: 155.82	Azimuth: 271.85
Hour: 20.00	Zenith: 170.80	Azimuth: 274.93
Hour: 21.00	Zenith: 174.08	Azimuth: 81.36
Hour: 22.00	Zenith: 159.13	Azimuth: 87.57
Hour: 23.00	Zenith: 144.14	Azimuth: 88.60

I have no idea if the results are correct but the values change so something is happening.

11

I knocked up this sketch...

FNNAAARR!

12

AWOL:

I knocked up this sketch...

FNNAAARR!

Maybe I should change it to 'banged out this sketch' instead XD

13

Actually, it doesn't. It moves relatively slowly.

Oh yeah ? Every passing minute brings the sun about 30,000 miles closer to star in the constellation Hercules, and there are still some misfits who insist that there is no such thing as progress.

14

I have no idea if the results are correct but the values change so something is happening.

The azimuth figures look plausible but the other column doesn't. And "zenith" is always up, the word you are looking for there is altitude or inclination.